First, a disclaimer. I do not consider myself an expert on the subject of boats planing, but more of an informed amateur with an engineering background who is interested in understanding how boats skim along on top of the water rather than plowing along through it. There might need to be a definition of planing but I have never found a consensus agreement among different designers, writers or other experts on just what constitutes the act of planing. Many books use speed/length ratios to determine if a hull is planing or not, but that is not satisfying since it only holds for boats that have nearly the same characteristics such as hull shape, weight, etc. For instance, at one end of the hull shape spectrum, the 16’ Hobie Cats and other multihulls can go fast enough to be considered planing by the speed/length definition, but they are achieving practically no lift from dynamic forces and are not even capable of planing on their knife blade hulls. At the other end of the spectrum, racing monohulls, step bottom hulls and three point hydroplanes go very fast and their speed/length ratio is meaningless. This last example demonstrates the point that beam of the planing surface is a far greater contributor to dynamic lift than waterline length. This follows in the same way that the luff length is more important in determining aerodynamic lift of a sail than the chord of the sail.
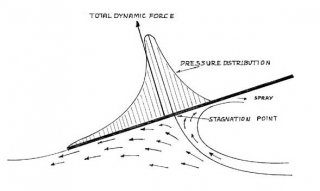
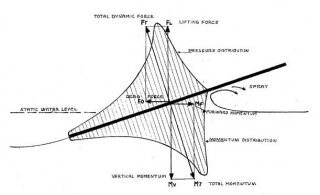
Although the flow diagrams shown in most books to illustrate planing phenomena may lead to the correct mathematical answer, I think they might obscure the physical events and inhibit understanding of the actual physics. They always show water flowing under a flat plate fixed at a positive angle of incidence to the water surface. I am not offering any new or different physics here, only a different way of looking at the same phenomena that may make it easier for the non-professional to understand it. The usual path shown in the books is to look at the water from the aspect of an observer in the boat. This makes it appear that the water is flowing under and past the hull. In reality, the water is doing no such thing. Here, we look at the same actions from the aspect of an observer in the water. The correct conclusion may be reached from either point of view but I think looking at the actual motion of the water makes it easier to understand the physics. Here we will go to Issac Newton’s fundamental principles of motion and try to think like a water molecule. Phil Bolger talks about a “sea of peas” and I think that may be close to what I am referring to. Of course, the water does not consist of peas but it may help to look at it that way. In any event, the water is just sitting there at rest until the inclined plate comes along. The moving plate hits the water and accelerates it in a vector normal (perpendicular) to the plate surface. This is down and forward. This motion makes room for the inclined plate to pass and the resulting momentum imparted to the water near the plate surface also makes the nearby water move down and a bit forward also, depending on the angle of incidence or trim of the flat plate. As the plate passes, the water particles rebound and set up damped oscillations that we see as waves. It also explains how the forward momentum imparted to the water by the inclination (trim angle) of the plate causes the surface of the water to rise to meet the plate at the forward edge. Water reacts to a stone dropped into the water by generating waves in much the same way. Of course, a boat is moving so the wave pattern is different but the forces are the same.
Looking to Newton again, it’s clear that the force imparting momentum to the water particles must have an exactly opposite force vector on the plate. This is the dynamic force vector of planing, also normal to the plate surface. This dynamic force vector is exactly equal and opposite to the force imparted to the water and may be resolved into the vertical lifting force and the normally smaller horizontal drag force. Efficient planing therefore becomes the effort to accentuate the former and minimize the latter forces. Because the water particles hit by the leading edge of the plate are already moving away by the time the next part of the plate arrives, momentum added to the water will therefore be reduced the further aft we go. To me, this explains the pressure diagrams shown in books although I think they are somewhat in error too. They usually show the magnitude of pressure asymptotic to, or nearly so, to zero at the trailing edge. That is not necessarily true although the shape of the hull bottom is all-important in this respect. The pressure may still be substantial right to the aft edge, beyond which, it must drop to zero. Addition of trim tabs or hull shape may introduce significant lift at the aft edge or transom.
The downward momentum of the water underneath the plate continues for a short distance aft of the plate and then rebounds with a damped oscillation motion. These are the standing waves that follow along at the same speed as the boat. Behind a flat bottom hull, these standing waves follow along directly behind the boat. Now, in V bottom boats, momentum imparted to the water also has a sideways component vector and the waves move more to the side from directly down in direct proportion to the deadrise angle. The energy consumed in pushing the water sideways by the angle of the V (deadrise) makes the V bottom boat a less efficient planing hull than the flat bottom one. There are, however, many good reasons for choosing a V bottom hull over a flat one. Someone experienced in observing these wave patterns might infer the angle of deadrise just from looking at the waves generated by the boat.
As an aside, a look at waves generated by a moving boat is interesting. It is easy to observe that the faster a planing boat moves, the lower the amplitude of the waves it generates. How can this be? The generation of these waves by a planing boat represents work done in supporting the weight of the boat. Work done has an element of time and is not a static measure. Provided the boat is planing, the work done on the water in supporting the fixed weight of the boat in a dynamic sense must be approximately the same over the same interval of time no matter what speed the boat is running. The “approximately” takes care of the fact that there may be a different amount of the boat weight supported by buoyancy at the different speeds. It takes less time for the boat to move a given distance at higher speed and so the work done in supporting the boat per unit of distance must be less at high speed than at lower speed. Therefore, it follows that waves made by a boat traveling at high speed will be of lesser height, carrying lesser energy, than the same boat planing at a lower speed.
That term, “dynamic lift”, is all-important and, to be called planing, a boat should be getting a significant portion of its lifting force from dynamic sources in addition to the buoyancy force. Just what portion of lift should be dynamic in order to define a boat as planing, I don’t know, but if the percentage is greater than 50%, we should be safe in saying that the boat is in the planing mode. I think the planing mode definition should hold well below 50% but don’t know where, or even if, a specific percentage should be chosen. In any event, such a definition would be far more satisfying than the usual ones of speed/length ratio, etc. We should not care a fig what it is called anyway, but rather expend our efforts in improving the planing ability of a boat intended for that service.
Now, given two boats of similar size, hull-form and weight, etc., the speed/length ratio can be used to compare their planing efficiencies. I hope this is not too obtuse a point but it is a bit like the speedometer in a car. It can measure how fast you are going and can be used to describe whether a car is fast or slow, but has nothing to do with how that speed was achieved. This bit of analog reasoning of the basic physics of planing satisfies me much more than pages of esoteric mathematical formulae and calculations. Of course, attention must be given to mathematic calculations to arrive at a satisfactory design but such calculations seldom create an understanding of the nature of the phenomena or lead to innovation.
Many readers will have noticed that there has been no mention of “hull speed” in the above analysis. That is a deliberate omission. I think that dwelling on hull speed formulae as an understanding of boat motion has been a great deterrent to innovative thinking. Such a formula is only useful in thinking about a narrow range of boat shapes. In particular, boats that are relatively heavy with curved or compound surfaces on the hull bottom. In such boats, the value of the “constant”, which is usually given as about 1.34, is a measure of the speed potential of that particular boat. For other similar boats, the “constant” must be changed, indicating that it is not really a constant at all. For other than purely displacement or semi-displacement boats, hull speed is only of marginal interest.
To illustrate the limitations of the hull speed formula, many boats are able to actually get on plane before the boat even reaches its “hull speed” as determined by its waterline length. The modern lightweight “sleds” as found in the around the world races zip right past their “hull speeds” without the slightest nod to the formula. Monohull powerboats can also meet this criteria with careful design and attention to weight. Given a good design, it is the bottom loading in pounds per square foot that determines the ease with which it will get on to plane. Lesser values of bottom loading is better in this regard and explains why the great majority of commercially available powerboats expend so much power and fuel in getting onto plane. They are generally too heavy for their bottom area to allow easy transition from displacement speed to planing speed. They require a high trim angle to generate adequate lift for planing and thus also need high power to overcome the higher drag generated by the high trim angle. It is a spiral that has only been overcome by the availability of high power engines and cheap gas. Such boats are only happy at very low or very high speed and are dinosaurs to many designers, including me. Length does play an important role in that the longer boat will have a higher hull speed, which may allow it to get on plane before that speed is reached so that the pilot of such a boat will be completely unaware that such a “hull speed” limitation exists.
Most texts describing hull speed will mention that hulls with a length/beam ratio of 10 or more are not limited by the rule. Most, but not all, multihulls fit in this category and are capable of speeds far in excess of theoretical hull speed and never plane while making such speeds. Such explanations evade the wide range of length/beam ratios between the “normal” 3:1 ratio of most monohulls and 10:1 or more of multihulls. I find the whole hull speed and speed/length thing unsatisfactory when talking about boats capable of planing. It may be useful in some circumstances but often does more harm than good.
To look at a specific example of how the above reasoning was applied, we will turn to a boat of my own design which is the featured boat of this website and with which I am most familiar. This is the Bluejacket 24, a small lightweight pilothouse cruiser intended for use on inland waters. It is primarily a planing boat that will plane with crew and full cruising gear at low power and readily hold plane down to about 10 or 11 mph. In light trim and ideal conditions with only one aboard, the Bluejacket 24 will actually clear the transom and appear to start to plane at about 9 1/2 mph. I will not venture to say that the boat is planing at this speed, but it is certainly beginning to do so. Throughout the speed range from 10mph to beyond 20mph, the attitude or trim angle of the Bluejacket 24 remains below 2 degrees and hardly changes at all. All increase in trim angle is in the bow as the stern does not sink or squat at all. As any regular powerboater can verify, the lack of stern squat is a desirable, although very rare, feature. A photo series of this performance can be seen in the Gallery page under Bluejacket 24.
In designing a boat, you can select any parameter, or set of parameters, that is/are most important and fix those, letting the other parameters be variable. A small cruising boat is primarily a people carrier, so I chose to fix the physical parameters to suit the people comfort goals first. Therefore, length, beam and interior height are chosen to begin with. From that, the displacement necessary to make those goals acceptable is calculated. Higher displacement is detrimental to economy of operation is a planing boat, so that consideration is wedded to all other design decisions. To satisfy the people comfort goal, the aft chines must be immersed to provide for adequate lateral stability. This dictates the maximum aft deadrise that can be used in order to keep the chines immersed. Forward deadrise must be greatly increased to make entry into chop and waves easier — the comfort thing again. Of course, this is too simplified and several laps around the specifications must be made before they are mutually complementary and individually acceptable. In a boat intended for other uses, say offshore, one would likely start with deadrise as one of the desirable fixed parameters.
In the above boat the displacement arrived at, with 2 crew and day trip gear, is 2500 lbs on a WL beam of 78” and an aft deadrise of 10 degrees. The aft buttocks are straight (monohedron) from the transom to about station 6 and rise forward to a sharp entry with deadrise of 26 degrees at a point 25% aft of the waterline entry. This has proven to satisfy all the design goals and handles a reasonable amount of chop and waves with ease. The local North Carolina waters are known for their nasty nature and these parameters appear to be at or near an optimum compromise between economy, performance and comfort.
I generally avoid concave sections near the bow as structurally weak and hard riding. Also avoided is any hint of longitudinally convexity in the aft planing bottom as a performance robber. There are exceptional cases like the Carolina Sports Fisherman boats that do use a bit of rocker near the stern to hold their sharp bow high when running in large waves. The only place I see concavity acceptable or desirable in a planing hull bottom is in keel, skeg, chine flat fairings or splash rails where the good properties outweigh the negative. In smooth water lake boats, like classic runabouts, the negative properties of bow section concavity are not always apparent since such boats are for pleasure use only and not required to operate in poor water conditions.
I am a retired electrical engineer and strictly an amateur boat designer. I work from paper sketches, calculators, testing models, all the good books I have found, discussions with other more and less experienced designers and my own reasoning. I have never gotten into computer design programs. As a result, my methods may appear antiquated, but they are the way I like to do it. The thinking and visualizing parts are what I like most about designing. Being only semi computer literate, I would like to learn something about that end of the work but have never devoted the necessary to time to do it.
Finally, here is another disclaimer. There are many established boat design parameters such as prismatic coefficient, displacement/length ratio, power/weight ratio, center of gravity (in all coordinates), center of floatation as well as many others that are important to designers of boats. I do not intend that this discussion should diminish the importance of any of these or other mathematical operations and my only purpose here is to aid the understanding of the physical forces that allow a boat to plane or allow one boat to plane better than another.
Trim angle of planing boats
One of the characteristics of powerboats that often puzzle boat operators is the trim angle of their boat and what causes it to be the value it is. Trim angle is the fore and aft angle in a vertical plane that the boat presents to the water surface. It is dependent on many factors, some of which can be controlled by the operator and some that are built into the design of the boat. The trim angle when the boat is at rest is simply the balance between the weight distribution of the boat and buoyancy distribution of the immersed part of the hull. The center of longitudinal gravity (CG) and the center of longitudinal buoyancy (CB) will always coincide on a boat at rest. When one changes, like shifting the CG by walking forward or aft, the CB will automatically shift to align itself with the CG.
When the boat is underway this changes and the CG may no longer align with the CB. This is the result of dynamic forces resulting from the motion of the boat. As long as nothing moves in the boat, the CG remains fixed while the CB moves (usually aft) as well as being combined with dynamic lift to give a new center of vertical force.
In making the decisions about performance characteristics of the Bluejackets, I wanted to design for a specific range of trim angle for what I think are good reasons. One major goal of my design was to have a boat that planed at low speed so that cruising could be pleasant and economical in the desired speed range of 10 to 20 MPH. Anyone who has had much experience with small powerboats knows that this speed range is generally the worst from both comfort and economic perspectives. From reading my notes of planning theory, you know that I consider weight to be the main killer of the desired performance so I’ll not repeat all that here. Suffice to say that weight, or more accurately bottom loading in weight per unit area of hull bottom, is the bugaboo of far too many planing powerboats and I wanted to avoid that.
While I generally ignore the concept of “hull speed” as being irrelevant to planing boat design, it is still a fact that all boats do start out from rest as displacement craft before accelerating to their operating speed and hull speed may be important in getting onto plane in the first place. “Hull speed” is an empirical way to look at the fact that a displacement vessel has a real limit to the speed that can be achieved because of the waves that it generates. Planing boats are the way to go much faster than that limited speed until speed is limited by other factors. Hull Speed varies proportionally with the length of the boat so, quite simply, holding the bow down when starting out makes the boat longer than if the bow lifted more, thus increasing the “hull speed”.
In order to achieve planing speed, adequate dynamic lift must be gained to get the boat higher in the water which reduces drag. Dynamic lift is proportional to both speed and trim angle. We can either force higher lift with more speed by adding driving power or reduce the need for lift by reducing weight. Meeting our economic goals requires that we take the lower weight path. At low angles, increasing trim angle increases lift, so we must have some degree of trim to get any lift at all. Trim angle also affects the comfort level in the boat. Running at high trim angle allows the water to first hit the boat bottom where it is flatter and results in uncomfortable pounding. Holding the bow down allows the sharper bow to strike the water first and causes less pounding and more comfort. Pounding is not a trivial factor and makes some boats extremely people unfriendly.
For best efficiency, it is generally accepted that a trim angle of four to five degrees minimizes total resistance from the sum of wave making and frictional drag although deep V hulls have higher optimum trim angle of 6 degrees or more. I am mostly concerned with boats that have low aft deadrise of 10 degrees or so which is also consistent with light weight. Further, it is a fact that high deadrise implies greater weight. Low trim angle reduces wave making resistance while high trim angle reduces skin frictional resistance. The most efficient trim angle for a boat is that which offers the least drag of combined wavemaking and friction. To satisfy my goals, four to five degrees of trim is too high. Boats that run at this angle will usually have a far higher trim while getting onto plane. To repeat, deep V means greater weight which is unacceptable to our goals. Another negative to high trim angle is that forward vision is restricted over the bow. In my opinion some boats have dangerously limited forward vision.
It should be clear that there are many conflicting factors here and choosing the combination that provides the desired result is how a designer moves toward the goal.
Bluejackets are designed and built lightweight and have large bottom surface, both of which contribute to low bottom loading, requiring minimal dynamic lift to initiate planing. This translates to the need for only a low trim angle when getting on plane and less power to do so. Heavier boats always need a higher trim angle to get adequate dynamic lift which requires higher power to overcome the resultant higher wave drag. Anyone who frequents boat building/design forums is familiar with the anguished questions from buyers of such heavy and high powered boats that have been unable to get them to plane satisfactorily. It is a vicious circle that I want to avoid.
In addition to the above factors, Bluejackets have high lift surfaces in the form of wide chine flats added under the stern. These chine flats have a trim angle that is greater than the rest of the aft bottom surface which provides extra lift aft and tends to hold the bow down and the stern up. Lifting the stern up also minimizes the drag associated with powerboats that have a deep transom causing high drag at low speed.
It is not possible to design or build a boat that is optimized in all the desirable characteristics at the same time since many are mutually exclusive. Improving one is almost always detrimental to one or more of the others. The best that can be accomplished is to choose which characteristics are most important for the operating regime and conditions that the boat is intended for. Bluejackets are primarily people carriers intended to be used mainly in inshore waters. Speed is important but some top speed can be sacrificed if it allows better performance in the speed range the boat will be used most in and we deem most important. Low trim angle increases frictional drag at high speed but also aids getting onto plane as well as economic operation at lower planing speed. I consider this a good trade since Bluejackets achieve top speeds that I consider very acceptable for a cruising boat.
If the Bluejacket were intended for regular operation in the open ocean, I would prefer a deeper V, more seakindly, hull but that would demand much more weight, power, fuel use, cost as well as larger towing vehicle and higher fuel use there also. That is not to say that Bluejackets cannot handle rough water but, rather that they are not optimized for that. Bluejackets have been used in some very rough water conditions as well as having made offshore passages and brought their crews home safely. Passages such as the Alaska Archipelago, West coast of Florida and New Jersey Coast are no problem with competent seamanship. The hull shape is a compromise between smooth riding in chop, efficient and economic power requirement, low fuel use and high load carrying ability. One inevitable factor is that many builders have added more weight than the plans dictate but the large foot print of the Bluejackets has allowed this with little loss in performance.
To sum this up:
Trim angle of a planing boat will always be that which is necessary to provide the required lift for the weight of the boat and the speed at which it is traveling.
Lower trim angle: more speed; greater planing surface area; CG further forward; lighter weight; lower aft deadrise.
High trim angle: lower speed; smaller planing surface; CG further aft; greater weight; higher aft deadrise.
Tom Lathrop
Oriental, NC